Vertical and horizontal slices on a 3D surface.
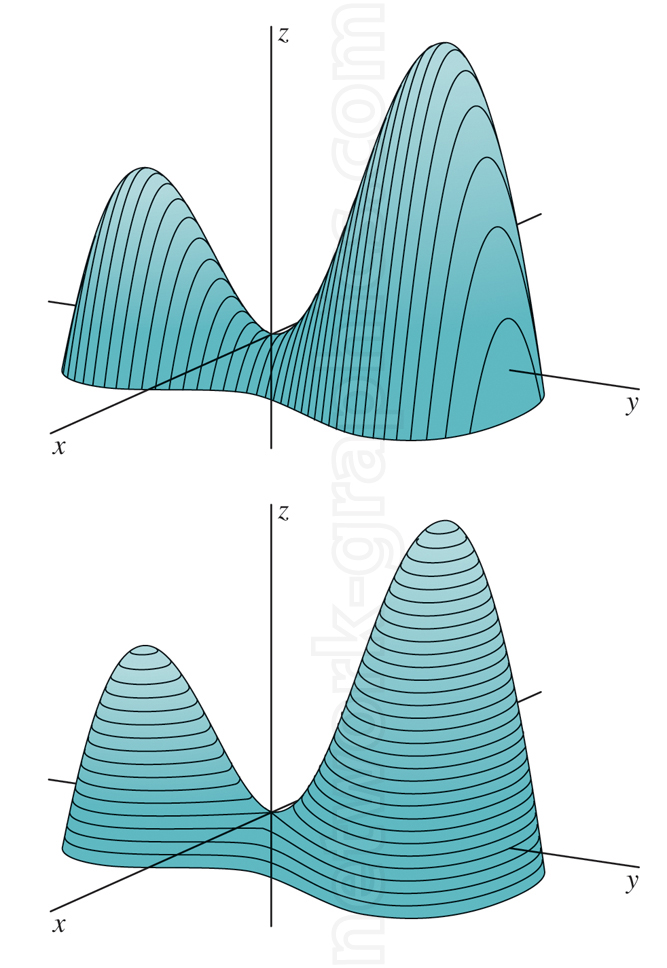
The 3D surface shown with vertical and horizontal slices.
The ‘lines can also hep describe the “topography” of the surface in space.
We can provide sample images or create custom illustrations tailored to your projects.
If you are looking for an illustration of this type, or from another subject area, you can contact us to discuss your needs.
Network Graphics / Division of Abramson & Wickham Graphics Inc.
All rights reserved.

