Solid and domain created from the intersection of a cylinder and plane.
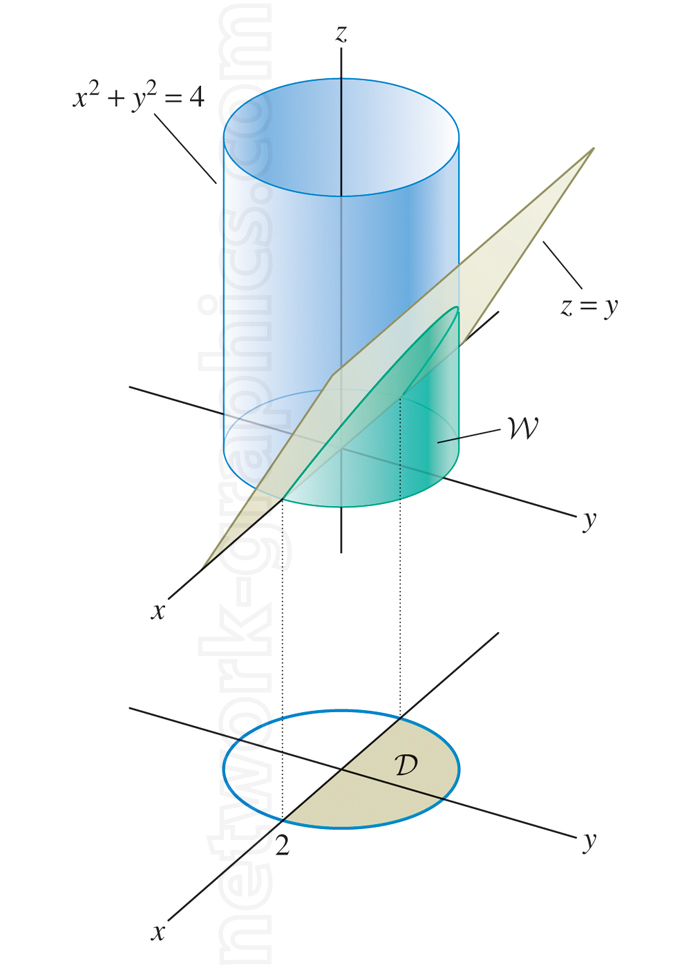
This diagram illustrates the intersection between a vertical cylinder defined by the equation x2 + y2 = 4 and an oblique plane given by z = y. The intersection forms a solid volume W on the surface of the cylinder, while the resulting domain D is projected as a partial circle on the xy-plane at z = 0. The visualization explores how geometric intersections yield bounded regions and new surfaces, essential for applications in calculus, 3D geometry, and vector calculus.
This graphic is ideal for use in multivariable calculus and analytical geometry textbooks, particularly when teaching volume integration, surface area calculations, and constraints in three-dimensional space. It demonstrates how algebraic equations of surfaces intersect in 3D space, generating complex regions suitable for further mathematical analysis through integration techniques or parametric representations.
We can provide sample images or create custom illustrations tailored to your projects. If you are looking for an illustration of this type, or from another subject area, you can contact us to discuss your needs.
Network Graphics / Division of Abramson & Wickham Graphics Inc.
All rights reserved.

